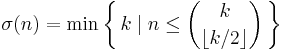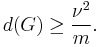Bipartite dimension
In the mathematical field of graph theory, the bipartite dimension of a graph G = (V, E) is the minimum number of bicliques, that is, complete bipartite subgraphs, needed to cover all edges in E. A collection of bicliques covering all edges in G is called a biclique edge cover, or sometimes biclique cover. The bipartite dimension of G is often denoted by the symbol d(G).
Contents |
Example
An example for a biclique edge cover is given in the following diagrams:
Bipartite dimension formulas for some graphs
The bipartite dimension of a 2n-vertex crown graph equals 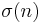 , where
, where
is the inverse function of the central binomial coefficient (de Caen, Gregory & Pullman 1981). Fishburn & Hammer (1996) determine the bipartite dimension for some special graphs. For example, the path 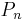 has
has  , the cycle
, the cycle 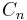 has
has  , and the complete graph
, and the complete graph 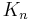 has
has  .
.
Computing the bipartite dimension
The computational task of determining the bipartite dimension for a given graph G is an optimization problem. The decision problem for bipartite dimension can be phrased as:
- INSTANCE: A graph
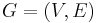 and a positive integer
and a positive integer  .
. - QUESTION: Does G admit a biclique edge cover containing at most
 bicliques?
bicliques?
This problem appears as problem GT18 in Garey and Johnson's classical book on NP-completeness, and is a rather straightforward reformulation of another decision problem on families of finite sets.
The set basis problem appears as problem SP7 in Garey and Johnson's book. Here, for a family 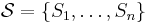 of subsets of a finite set
of subsets of a finite set 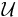 , a set basis for
, a set basis for  is another family of subsets
is another family of subsets 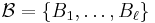 of
of 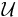 , such that every set
, such that every set 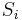 can be described as the union of some basis elements from
can be described as the union of some basis elements from 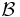 . The set basis problem is now given as follows:
. The set basis problem is now given as follows:
- INSTANCE: A finite set
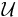 , a family
, a family 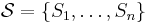 of subsets of
of subsets of 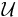 , and a positive integer k.
, and a positive integer k. - QUESTION: Does there exist a set basis of size at most
 for
for  ?
?
In its former formulation, the problem was proved to be NP-complete by Orlin (1977), even for bipartite graphs. The formulation as a set basis problem was proved to be NP-complete earlier by Stockmeyer (1975). The problem remains NP-hard even if we restrict our attention to bipartite graphs whose bipartite dimension is guaranteed to be at most 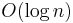 , with n denoting the size of the given problem instance (Gottlieb, Savage & Yerukhimovich 2005). On the positive side, the problem is solvable in polynomial time on bipartite domino-free graphs (Amilhastre, Janssen & Vilarem 1997).
, with n denoting the size of the given problem instance (Gottlieb, Savage & Yerukhimovich 2005). On the positive side, the problem is solvable in polynomial time on bipartite domino-free graphs (Amilhastre, Janssen & Vilarem 1997).
Regarding the existence of approximation algorithms, Simon (1990) proved that the problem cannot be approximated well (assuming P ≠ NP). Indeed, the bipartite dimension is NP-hard to approximate within 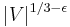 for every fixed
for every fixed 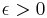 , already for bipartite graphs (Gruber & Holzer 2007).
, already for bipartite graphs (Gruber & Holzer 2007).
In contrast, proving that the problem is fixed-parameter tractable is an exercise in designing kernelization algorithms, which appears as such in the textbook by Downey & Fellows (1999). Fleischner, Mujuni & Szeider (2009) also provide a concrete bound on the size of the resulting kernel, which has meanwhile been improved by Nor et al. (2010). In fact, for a given bipartite graph on n vertices, it can be decided in time 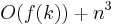 with
with 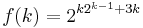 whether its bipartite dimension is at most k (Nor et al. 2010)
whether its bipartite dimension is at most k (Nor et al. 2010)
Bounds
Although determining the bipartite dimension is computationally hard, quite a few estimates are available. For instance, Jukna & Kulikov (2009) established a relation between the size of a maximum matching and the bipartite dimension. More precisely, they showed that for a graph G with m edges that admits a matching of size 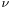 the following holds:
the following holds:
Applications
The problem of determining the bipartite dimension of a graph appears in various contexts of computing. For instance, in computer systems, different users of a system can be allowed or disallowed accessing various resources. In a role-based access control system, a role provides access rights to a set of resources. A user can own multiple roles, and he has permission to access all resources granted by some of his roles. Also, a role can be owned by multiple users. The role mining problem is to find a minimum set of roles, such that for each user, his roles taken together grant access to all specified resources. The set of users together with the set of resources in the system naturally induces a bipartite graph, whose edges are permissions. Each biclique in this graph is a potential role, and the optimum solutions to the role mining problem are precisely the minimum biclique edge covers (Ene et al. 2008).
A similar scenario is known in computer security, more specifically in secure broadcasting. In that setup, several messages need to be sent each to a set of receivers, over an insecure channel. Each message has to be encrypted using some cryptographic key that is known only to the intended receivers. Each receiver may possess multiple encryption keys, and each key will be distributed to multiple receivers. The optimum key generation problem is to find a minimum set of encryption keys for ensuring secure transmission. As above, the problem can be modeled using a bipartite graph whose minimum biclique edge covers coincide with the solutions to the optimum key generation problem (Shu, Lee & Yannakakis 2006).
See also
- List of NP-complete problems
- Intersection number (graph theory), the minimum number of cliques needed to cover the edges of a graph
References
- Amilhastre, Jérôme; Janssen, Philippe; Vilarem, Marie-Catherine (1997), "Computing a minimum biclique cover is polynomial for bipartite domino-free graphs", Proceedings of the Eighth Annual ACM-SIAM Symposium on Discrete Algorithms, 5–7 January 1997, New Orleans, Louisiana., ACM/SIAM, pp. 36–42, http://portal.acm.org/citation.cfm?id=314175
- de Caen, Dominique; Gregory, David A.; Pullman, Norman J. (1981), "The Boolean rank of zero-one matrices", in Cadogan, Charles C., 3rd Caribbean Conference on Combinatorics and Computing, Department of Mathematics, University of the West Indies, pp. 169–173, MR0657202.
- Downey, Rod; Fellows, Michael R. (1999), Parameterized complexity, Springer, ISBN 0-387-94883-X.
- Ene, Alina; Horne, William G.; Milosavljevic, Nikola; Rao, Prasad; Schreiber, Robert; Tarjan, Robert Endre (2008), "Fast exact and heuristic methods for role minimization problems", in Ray, Indrakshi; Li, Ninghui, 13th ACM Symposium on Access Control Models and Technologies (SACMAT 2008), ACM, pp. 1–10.
- Fishburn, Peter C.; Hammer, Peter L. (1996), "Bipartite dimensions and bipartite degrees of graphs", Discrete Mathematics 160 (1–3): 127–148, doi:10.1016/0012-365X(95)00154-O.
- Fleischner, Herbert; Mujuni, Egbert; Paulusma, Daniël; Szeider, Stefan (2009), "Covering graphs with few complete bipartite subgraphs", Theoretical Computer Science 410 (21-23): 2045–2053, doi:10.1016/j.tcs.2008.12.059.
- Garey, Michael R.; Johnson, David S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, ISBN 0716710455.
- Gottlieb, Lee-Ad J.; Savage, John E.; Yerukhimovich, Arkady (2005), "Efficient data storage in large nanoarrays", Theory of Computing Systems 38 (4): 503–536, doi:10.1007/s00224-004-1196-9.
- Gruber, Hermann; Holzer, Markus (2007), "Inapproximability of Nondeterministic State and Transition Complexity Assuming P <> NP.", in Harju, Terjo; Karhumäki, Juhani; Lepistö, Arto, 11th International Conference on Developments in Language Theory (DLT 2007), LNCS, 4588, Turku, Finland: Springer, pp. 205–216, doi:10.1007/978-3-540-73208-2_21.
- Jukna, Stasys; Kulikov, A. S. (2009), "On covering graphs with complete bipartite subgraphs", Discrete Mathematics 309: 3399–3403, doi:10.1016/j.disc.2008.09.036.
- Monson, Sylvia D.; Pullman, Norman J.; Rees, Rolf (1995), "A survey of clique and biclique coverings and factorizations of (0,1)-matrices", Bulletin of the ICA 14: 17–86, MR1330781.
- Nor, Igor; Hermelin, Danny; Charlat, Sylvain; Engelstadter, Jan; Reuter, Max; Duron, Olivier; Sagot, Marie-France (2010). "Mod/Resc Parsimony Inference". arXiv:cs.DS/1002.1292..
- Orlin, James (1977), "Contentment in graph theory: covering graphs with cliques", Indagationes Mathematicae 80 (5): 406–424, doi:10.1016/1385-7258(77)90055-5.
- Shu, Guoqiang; Lee, David; Yannakakis, Mihalis (2006), "A note on broadcast encryption key management with applications to large scale emergency alert systems.", 20th International Parallel and Distributed Processing Symposium (IPDPS 2006), IEEE.
- Simon, Hans-Ulrich (1990), "On Approximate Solutions for Combinatorial Optimization Problems", SIAM Journal on Discrete Mathematics 3 (2): 294–310, doi:10.1137/0403025.
- Stockmeyer, Larry J. (1975), The set basis problem is NP-complete, Technical Report RC-5431, IBM.